2023あたり
最近は、DEFCON CTF 30のためと言い訳して買ったベアボーンPCに適当にCPUとかを刺したあと、それにProxmox VEをインストールしてUbuntu Cloud Imageをcloud-init設定で立ち上げてTailscaleとK3sとRcloneをインストールしてSmokePingとかを立ち上げて遊んでいます。OPNsenseとかも動いています。適当なVPSを借りて、MinIOをインストールしてレプリケーションを組んでみたり組んでみなかったりしても遊んでいます。MongoDBもずっと動いています。本もまあまあ読みました。ブクログに全部登録して、時々CSVエクスポートしてどこかに保存しています*1*2*3。Obsidianの使い方も一番基礎を覚え始めました。まあまあ元気です。
*1:本自体が大事なのは間違いありませんが、最近は紙の書籍がどうこうとか、DRMなどという話もあることを考えると、一般の書籍については、読んだような気がする記憶と抱いたような気がする感想とISBNなどといったポインタ情報が大事なんじゃないかと思うこの頃です。国会図書館などに期待できそう。論文や、PDFダウンロードした書籍などは、最近Zoteroに保存し始めてもいますが。Zoteroはストレージに任意のWebDAVを指定することが可能です。
*2:僕は昔から、教科書に蛍光ペンなどを全然使わない人でした。書籍の内容なんて覚えていられません。自分にとって、書籍とは、事前条件が満たされたときに読み切ると事後条件が満たされる、契約プログラミング的な捉え方をしているものな気がします。学校の課程とは、その事前条件と事後条件が筋良くつながり続けるよう設計された、科目の連続体のような気がします。
*3:ちょっと別の学科の授業を受けてなにも意味が分からなかったときの絶望感といったら、もう
Ricerca CTF 2023 Writeup (NEMU, Rotated Secret Analysis)
Ricerca CTF 2023にチーム TSG-graduates で参加しました。4位でした。
Ricerca CTF 2023は賞金獲得要件に「日本国内在住である学生のみで構成される」があるので、それに適合しない人々の集まりです。日本国内在住である学生の人たちがチーム TSG で参加をしており、あちらはあちらで盛り上がっていたようです。*1
🏁Ricerca CTF 2023 終了🏁
— 株式会社リチェルカセキュリティ (@RicercaSec_JP) April 22, 2023
本日 4 月 22 日(土)午後 10 時をもって #RicercaCTF 2023 は終了しました。
ご参加くださり、誠にありがとうございました。 pic.twitter.com/Qi0APWhPsg
BOFSec, Rotated Secret Analysis, NEMUあたりを解きました。NEMUとRotated Secret Analysisのwriteupを書きます。
NEMU
すごい。あのC言語が、GCC拡張で関数内関数定義なんて許すんですね。知らなかった。
https://gcc.gnu.org/onlinedocs/gcc/Nested-Functions.html
ソースコードを少しにらむと、r1, r2, r3, aの定義はint32_tなのに、load,mov,...の引数はuint64_tとなっており、サイズ不一致が起きていることがわかります。特にuint64_t*を受け取ってそこに書き込みを行うmov, inc, dblで破壊を行えることに気づきます。
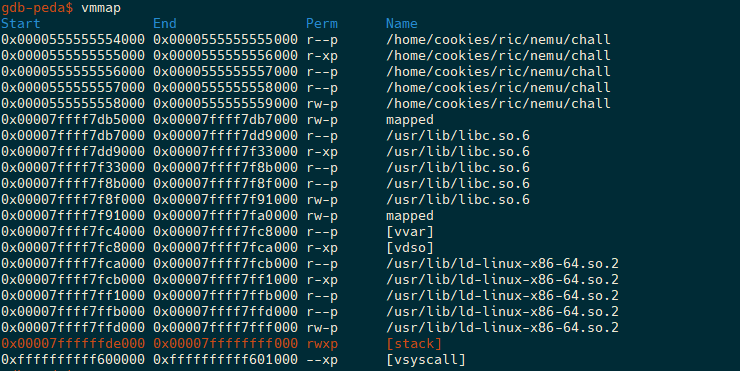
ここで破壊可能なのは(32bitの)r1, r2, r3, aそれぞれの直後に位置する32bitな訳ですが、これをGhidraやgdbで確認すると、実際の所r1の直後32bitの値であることが分かります。
 gyazo.com
gyazo.com
 gyazo.com
gyazo.com
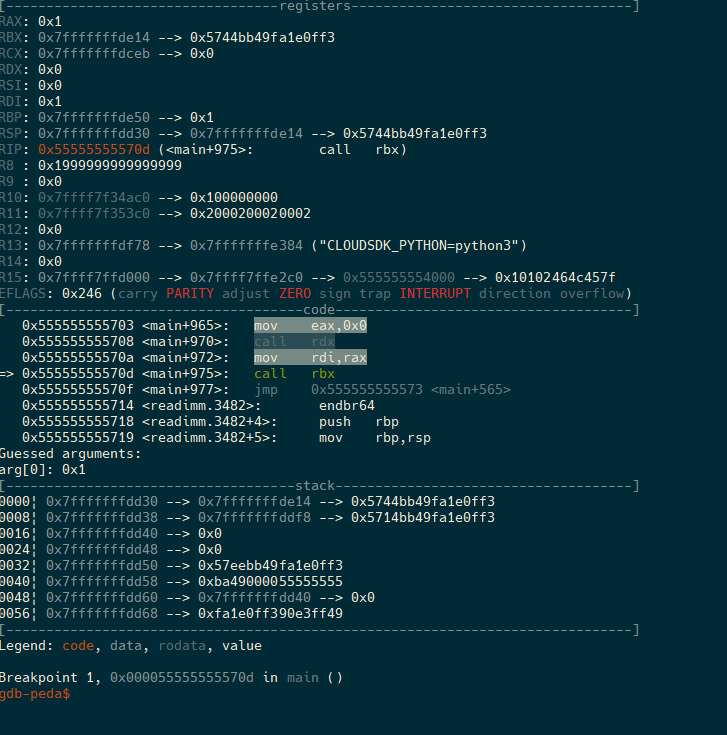
gdb上のstack領域0x7fffffffdd40から16byteが、4つの32bit register用領域で、その直後0x7fffffffdd50から4byteが、破壊可能箇所です。ここに今なにがあるのか気になります。一見ランダムな値に見えますが、どうも機械語っぽいような気もします。逆アセンブルしてみます。
かなり機械語っぽいです。でも待てよ、ここってstack領域なはずだぞ?
なんてこった、このELF、stack領域が実行可能だ。わざわざこんなことするとも思えないので、きっと関数内関数定義を使った副作用なんでしょう。今main.cをgccでコンパイルしてみたら、ちゃんとldが警告出してきました。
$ gcc main.c /usr/bin/ld: warning: /tmp/ccg7DhQI.o: requires executable stack (because the .note.GNU-stack section is executable)
強い情報を得ました。stackは実行可能で、そしてそこを4byteだけですが書き換え可能ということです。ここっていつ実行される命令列なんでしょう。ちょっと調べてみると、この0x7fffffffdd50は、add関数へのtrampolineであることが分かります*2。同様にして、0x7fffffffdd6cからaddiへのtrampoline、0x7fffffffdd88からdblへのtrampolineがあることが分かります。
ENDBR64命令は、実際の所なんなのかよく知りませんが、各関数の一番始めについていがちで、いつも読み飛ばしています。きっと深淵な存在意義はあるのでしょうけど、まあだいたいNOPです。たぶん。怒られる。
ENDBR64の位置を破壊すると、add NEMU命令を呼ぶたびに、直前に好きなことができるようになります。4byteだけですが、なにをしましょうか。いろいろ考えた結果、PUSH rdiを入れておくと良い感じになると結論づけました。
main関数から、CALL rbxでtrampolineに飛んできて、rdiに関数内関数定義済み関数への第一引数が飛んできて、addの場合はregisterのアドレスがやってきます。ここでPUSH rdiをしておいて、trampoline jump先からRETするときに、PUSHしておいたregister値の格納先stack領域アドレスにripが移ります。stack領域は実行可能なので、registerに適切な機械語さえ入れておけば、問題なく実行が行えます。registerに入れておく機械語の最後にRETを入れておくと、うまく整合してmain関数のもとの位置(CALL rbx直後)にripが戻り、なにごとも無かったかのように実行を続けることが出来ます。
この作業によって、少なくともr3とr2の8byte - RET用1byte = 7byte、自由に機械語を実行できるようになりました。7byteもあったらだいたいの1手作業は行えて、それを繰り返し可能です。
この7byteの自由空間を使って、addi用trampolineコード周辺の改ざんを行いました。いつものshell-stormさんからもらってきた*3 27byteシェルコードに置換を行いました。これ以降、addi NEMU命令は使用不可能になりますが、別に要らないでしょう。ギリギリdbl用trampolineコードまでは食わないようです。別に食っても問題なかったですが。
最後にaddi NEMU命令を実行して、addi用trampolineコード箇所にあるシェルコードを実行して、シェルが取れて終わりです。
ローカルではexpect 'opcode:'なるプロンプト待ちを入れていたのですが、リモートで実行したら永遠に終わらなかったため、このwaitはコメントアウトしました。CTF pwn問題、ほんとに、network越しのI/O bufferingがかかわってくるとめちゃくちゃ面倒になるので、今回のような決定的なI/O処理は本当にえらいですね~~ 一切プロンプト待ちを行わなくても動く。
コードは以下になります。
gist.github.com
Rotated Secret Analysis
RSAで、ただしN = pqのpとqが、512bit rotated関係にあります。
pとqの関係性を利用して、Nの素因数分解を考えます。p = 2**512 a + b (a, bは512bit以下)と表したとき、q = 2**512 b + aと表せて、つまりN = pq = (2**512 a + b)(2**512 b + a)と表せるでしょう。
2048bitのNの下位512bitおよび上位512bitを取れば、abの値が、繰り上がりを考慮した数bitのずれを許した上で、ほとんど正しく求まります。
abの値を仮定すれば、Nからaa+bbも算出できます。(a+b)^2を構成すれば、a+bも算出できます。abとa+bが分かったとき、aおよびbの算出は、二次方程式の解と係数の関係*4から、二次方程式の解の公式で行えます。
コードは以下になります。
gist.github.com
問題を作ってくれて、開催してくれて、一緒に参加してくれて、writeupを読んでくれて、ありがとうございました。
*1:2チーム間での情報の分断のため、各々用のSlack private channelを用意しました。また、情報共有のため、いつも使いがちなツールは使わずに、古き良きGoogle Docsを利用しました。HackMDでも良かったかもしらんが、思いつかなかった。
*2:trampolineっていうのは正確な定義は知りませんが、OS Kernelの実装とかで出てくるあれです、 https://en.wikipedia.org/wiki/Trampoline_(computing) Wikipediaを読んで雰囲気を感じてくれ
*3:いつもありがとう。
*4:どうでもいい話ですが、高校生のときに友人から聞いた話で、一部の塾だか界隈では「解と計数の関係より」と百回も一万回も書くのが面倒なので、界隈内用語として「かけかより」という略語が通用するそうです。真実は知りません。かわいくないですか?
BusyBox(Alpine Linux)でone_gadgetはうごかない
CTF pwnネタです。古いやつ。
数年前に気づいたんですが、急に思い出して、なんとなく記事にしてみることにしました。古い話だし全然CTF最近してないので、今どれくらい通じる話か知りません。最近はカーネル問が流行ってそうだからだいぶ役に立たなさそう。
↑というところまで書いた下書き記事がはてなブログに保存されてから、また数年経ちました。雑に完成させて公開するぞするぞ。
前提知識
one gadget
CTF pwn文脈において、まず「one gadget」という概念があります。簡単にまとめておきます。
「RIPをとる」(x86ならEIP)(より一般にはProgram Counter)という感覚はもうpwn界において十分知られていると思いますが、RIPが取れた後に、「シェルをとるにはどうするか」ということに頭を悩ますことがあります。そこでのひとつのテクニックがone gadgetです。かなり容易に満たされ得る条件(e.g. スタックトップから少し下がNULLである、RCXがNULLである)だけの制限で、RIPを「特定のアドレス」(そこから始まる一連のロジックをone gadgetと呼びます)にできさえすれば、シェルが立ち上がってくる、というものです*1。
david942j/one_gadgetが、特定のlibc (バージョンの違いを含め)に対してone gadgetを探すのに使えるツールです。
本編
one gadgetのしくみ
one gadgetは、ぱっと見かなり魔法なのですが、どうやって動いているのでしょうか。
まず、通常のshellcodeが何をしているかを思い出しましょう。min-caml pwnのときもお世話になったshell-storm #827なんかもそうですが、結局、"/bin/sh"を第1引数に、第2, 第3引数をうまいことargv, envpっぽくして、execve syscallを発行する、みたいな感じです。
RIPをとったあとは、これを実行するべく、shellcodeをrwx領域に書き込んで実行したり、"/bin/sh"だけどうにかしてsystem関数へret2libcしたり、ROPをがちゃがちゃやったりするわけです。
one gadgetは、この動作を勝手にやってくれるアドレスを見つける、という行為です。そんなに運がいい場所がたまたまあるのかというと、まあ、よく考えると少なくともsystem関数の中のフローを解析して、全機械語単位からの動作をシミュレーションしてみれば、ありそうな気はします。少なくともsystem関数の実装のために"/bin/sh\0"という文字列はglibcに埋まっています。
system関数の先頭アドレスがone gadgetとなれないのは、第一引数の制限が厳しいからです。system関数は、第一引数を、["/bin/sh", "-c"]に続けて挿入し、execve syscallを発行する、というような挙動をします。ですからsystemへの第一引数(x86ならstack top、x64ならrdi)はNULLでも空文字列へのポインタでもだめで、最低"sh"へのポインタとかでないとだめなわけです*3。
david942j/one_gadgetが見つけてくるone gadgetは、だいたい、続く処理が最終的にexecve(path="/bin/sh", argv=NULL, envp=NULL)みたいなのをexecするための、開始地点とそのときの制約条件を出力します。
この辺でargvがNULLであるかNULLへのポインタを指しているかなどを調べています:
https://github.com/david942j/one_gadget/blob/6dc634daba06792badd5260d02395780f2eaed5c/lib/one_gadget/fetchers/base.rb#L97-L113
この辺にx64の簡易エミュレータを持っています:
https://github.com/david942j/one_gadget/blob/6dc634daba06792badd5260d02395780f2eaed5c/lib/one_gadget/emulators/x86.rb#L37
ざっとRubyコードを読んだ感じ、たぶん、objdump -Dの結果からexecをgrepしてきて、その直前30行をとってきて、それぞれの行から簡易エミュレータを動かしてみてexecの行まで達したときに、argvやenvpがNULLになるみたいな条件を満たすための制約を出す、みたいな実装っぽいです。
/bin/shに-c含めコマンドラインオプションが一切渡されなかったとき、単純にシェルが起動するので、CTF pwnの「シェルを取る」が達成できたね、めでたし、になります。
BusyBoxの仕組み、あるいはシングルバイナリの仕組み
一旦one gadgetのことは忘れて、BusyBoxの仕組みについて考えましょう。
BusyBoxの何が非自明かというと、シングルバイナリがどうやって動いているかです。上でbusybox ls -lをするとls -lが動くと書いたけれど、そんなbusyboxを動かすときに毎回busyboxって打ってますか?普通、busyoxを使うときは、busyboxバイナリのコピーを大量に/binに生やすはずです。シンボリックリンクでもハードリンクでもファイルコピーでもいいですが。
$ docker run --rm busybox sh -c 'sha1sum /bin/*' | head 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/[ 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/[[ 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/acpid 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/add-shell 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/addgroup 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/adduser 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/adjtimex 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/ar 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/arch 16ce3cb4f2c5fe3f12de55cb7262a839292563ac /bin/arp
全部おんなじファイルですね。まあこれハードリンクなんですけど。
docker run --rm busybox sh -c 'stat /bin/arp /bin/acpid' File: /bin/arp Size: 1025504 Blocks: 2008 IO Block: 4096 regular file Device: 38h/56d Inode: 2120300 Links: 401 Access: (0755/-rwxr-xr-x) Uid: ( 0/ root) Gid: ( 0/ root) Access: 2022-11-17 20:00:00.000000000 +0000 Modify: 2022-11-17 20:00:00.000000000 +0000 Change: 2022-12-17 01:54:57.807497313 +0000 File: /bin/acpid Size: 1025504 Blocks: 2008 IO Block: 4096 regular file Device: 38h/56d Inode: 2120300 Links: 401 Access: (0755/-rwxr-xr-x) Uid: ( 0/ root) Gid: ( 0/ root) Access: 2022-11-17 20:00:00.000000000 +0000 Modify: 2022-11-17 20:00:00.000000000 +0000 Change: 2022-12-17 01:54:57.807497313 +0000
じゃあ全く同じバイナリを/bin/arpと起動したときと/bin/acpidと起動されたときとで挙動を変えなければならなくて、どうやるの?という話になります。
これは典型的なテクで、argv[0]を使うというやつです。
シェルにコマンドを渡して実行するとき、普通起動バイナリのパスを一番最初に置くと思いますが、どこの慣習なのか仕様なのか標準なのかは知らないんですがargv[0]もそれに対応して実行可能ファイルのパスになっていがちです。
busyboxではこのargv[0]を利用してどういう起動のされ方をされたかを調べて、それをapplet名として期待された機能を果たしています。コードはたぶんこのへん: https://github.com/mirror/busybox/blob/02ca56564628de474f7a59dbdf3a1a8711b5bee7/libbb/appletlib.c#L1107-L1128
BusyBoxでone_gadgetは動かない。
ということでタイトル回収です。
one_gadgetは基本的にexecve("/bin/sh", argv=NULL, envp=NULL)のような点を探します。このときはargv[0]は存在しません。というかargvがNULLなのでアクセス違反です。
BusyBoxはargv[0]でappletの判断を行います。
よって、/bin/shがBusyBoxであったとき、one_gadgetは動きません。 ←結論
ただ、実は(CTFにおいて)あまりこれが問題になることはなかったりします。
そのひとつはたぶん、「one_gadgetはたいてい、glibcにしか効かない。BusyBoxのような極限環境の場合、あんまりglibcが動いてることはない。muslとかが多いがち。」
BusyBoxの利用者のひとつとして、記事タイトルの通り、Alpine Linuxがあり、Alpine Linuxでone gadgetが動かなかったので謎に思って100年前に調査した結果の記事なのでした。
*1:ぼくは「うさぎ小屋」 https://kmyk.github.io/blog/blog/2016/09/16/one-gadget-rce-ubuntu-1604/あたりで初めてノリを知りました。
*2:busyboxを持ってない状態でbinを消し飛ばすと... wgetもcurlもなくてどうしようね
*3:-cに続くargumentがなければコマンドラインオプションパースエラーだし、空文字列なら無を実行してすぐ戻ってきてしまいます。
*4:ちなみに、Linuxくんどうやってるのかあんまり知らないですが、psの表示名を書き換えるためにargv[0]を書き換えるというテクというのも存在しますね: https://higepon.hatenablog.com/entry/20050706/1120646217
new Slack appへの移行のはまりどころとか
この記事はTSG Advent Calendar 2022のN日目の記事です。N=17になりました。
adventar.org
ブログの書き方を忘れかけています。思い出すためにがんばります。
Slack appでclassic Slack appからnew Slack appに移行した話です。大分前なこともあり、できるだけ根拠へのリンクを含めたとはいえ嘘とかも含まれると思います。間違いがあったらちょっと申し訳ない気持ちにはなりますが、責任は負いません。
続きを読むSlackのClassic AppをNewer App with granular scopesに更新したので飯がうまい
— こおしいず(っ'ヮ'c) (@kcz146) August 30, 2022
Chromeのブックマークを1フォルダ晒してみる
きっと他人のブラウザブックマークを覗き見るのって楽しいと思うんだよね。10年以上かけてできたものなわけで、きっと出会いを創出できると思うんだ。
わりかしなんびとにも便利そうな、ブックマークバーの「onlinetools」っていう名前のフォルダから、よくなさそうなものを除いて、上から置いていくよ。古い順とも新しい順ともわからないよ。
[リンク切れ]って書いてあるリンクには飛ばない方がいいよ。変なページにリダイレクトされたりするよ。
リンク切れじゃなくても、リンク先の安全性は保証しないよ。
Find More Words - Find your Scrabble cheat words for Scrabble or Words with Friends
なんだろうね。登録した覚えがないね。Scrabble別にそんなに好きじゃないし、0.3回くらいしかしたことないのにね。CTFでFLAGが90%くらいわかってるときに、残りを推測で当てるために使ったような気もしてきた。
Graphing Calculator
desmos。グラフ({(x,y) \in R^2 | f(x,y)=0}系の意味の)図示ツール。
これは受験生に必須だね。tを使うと媒介変数表示もグラフできたり、境界線を含んだり含まなかったりする領域まで図示できちゃったりするの、本当に偉い。
xy平面の図形を極座標上に変換した時の変域の話 - cookies.txt .scr←たしかこの記事も、desmosを見ながら書いたような気がする。
Wolfram|Alpha: Computational Intelligence
wolframalpha。紹介するまでもないね。
受験生もそうだけど、大学生になってからも必須だね。数IIIの積分とかで、当たると答えがわかってよいね。当たらないと仕方ないから自分で考えるしかないね。
Online Alarm Clock
ただの目覚まし。
訳がわからないけど、まともな時計の目覚ましを使わずに、電気入れっぱなしのノートパソコンでこれを鳴らしてたときがあったような気がするね。わけがわからないね。